baltimorespot.blogg.se

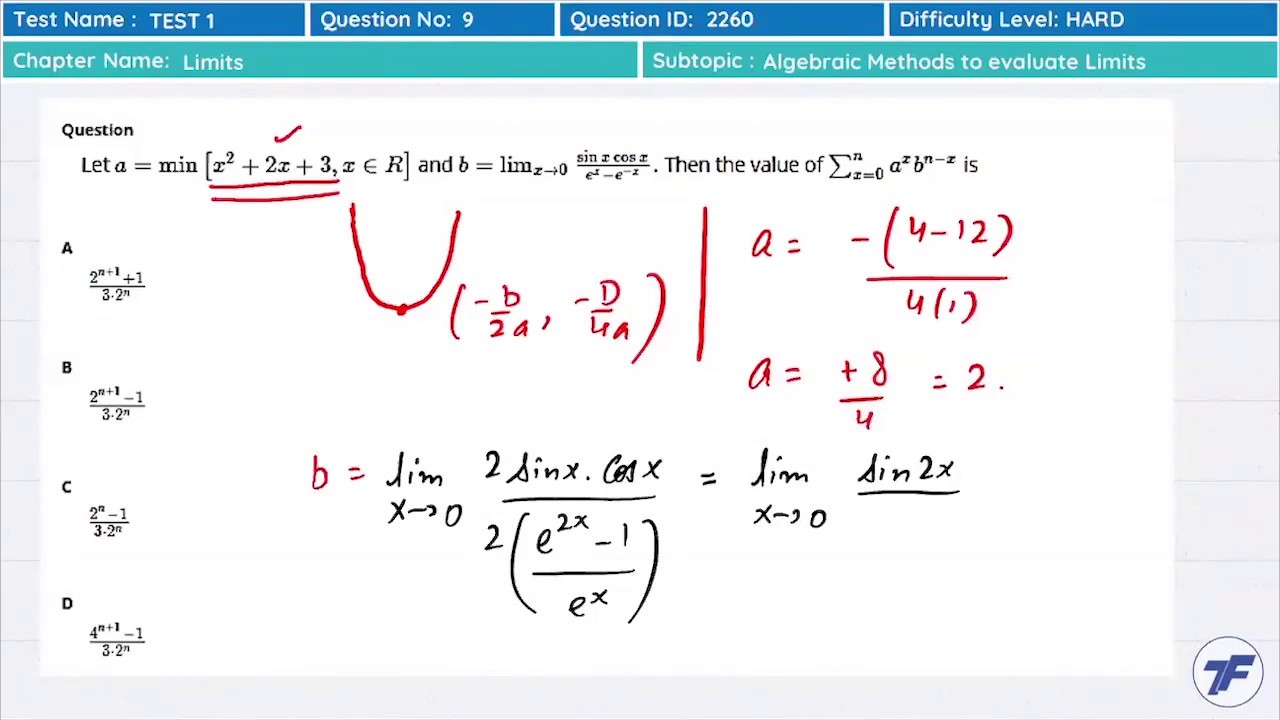
In the previous example, we saw that even though 𝑓 ( − 9 ) = − 7, its limit as Since the left and the right limit of 𝑓 ( 𝑥 ) both exist and are equal This means that their limits as 𝑥 approaches − 9 from the right must We will start with l i m  →    𝑓 ( 𝑥 ). This function as 𝑥 approaches − 9 by checking that the left and the right Since this is a piecewise-defined function and 𝑥 = − 9 is on the boundary of two subdomains, Hence, l i m  →  𝑓 ( 𝑥 ) exists and equals 4.Įxample 3: Finding the Limit of a Piecewise-Defined Function at a Point 𝑥 = 3 exist and they are both equal to 4. Therefore, we have shown that the left and the right limit of 𝑓 ( 𝑥 ) at Not when 𝑥 is arbitrarily close to 3 from the right: Inside of the limit, since it only affects the value of the function when 𝑥 = 3, Recall that we can cancel shared factors of 𝑥 − 3 in the numerator and denominator This is an indeterminate form, so we will need to simplify the rational function by factoring. Since this is a rational function, we can attempt to evaluate this by direct substitution:ģ + 6 ( 3 ) − 2 7 ( 3 ) − 3 ( 3 ) = 0 0. Next, to evaluate l i m  →   𝑓 ( 𝑥 ), we can notice that whenģ < 𝑥 < 9, we have 𝑓 ( 𝑥 ) = 𝑥 + 6 𝑥 − 2 7 𝑥 − 3 𝑥   this gives us

We can evaluate the limit of absolute value functions by direct substitution, giving us So we can assume that − 2 < 𝑥 < 3, without affecting the value of the limit.

When evaluating this limit, the values of 𝑥 will get arbitrarily close to 3, To evaluate the limit as 𝑥 approaches 3 from the left, we note that when This function as 𝑥 approaches 3 by checking that the left and right limits of Since this is a piecewise-defined function and 𝑥 = 3 is on the boundary of two subdomains, In our next few examples, we show the existence and find the value of the limit of a piecewise functionĪt a point on the boundary of its subdomains.Įxample 2: Discussing the Existence of the Limit of a Piecewise-Defined Function at a Pointĭiscuss the existence of l i m  →  𝑓 ( 𝑥 ) given Hence, the limit does not exist because l i m l i m  →   →    𝑓 ( 𝑥 ) ≠ 𝑓 ( 𝑥 ). However, we have shown that they are not equal. įor the limit of 𝑓 ( 𝑥 ) at 𝑥 = 7 to exist, both the leftĪnd right limits need to be equal. ] 7, 8 [ does not affect the value of the limit, giving us We can do the same for the right limit restricting the values of 𝑥 to be in the interval We can evaluate this by direct substitution: When our values of 𝑥 are in this interval, Without affecting the value of the limit. 𝑥 will get arbitrarily close to 7, so we can assume 1 < 𝑥 < 7, We have 𝑥 < 7 for our input values and when evaluating this limit the values of We start with l i m  →   𝑓 ( 𝑥 ), since this is a left limit This function as 𝑥 approaches 7 by checking that the left and right limits of Instead, we recall that we can determine the limit of We cannot evaluate this limit by direct substitution. Since this is a piecewise-defined function and 𝑥 = 7 is on the boundary of two subdomains, Example 1: Discussing the Existence of the Limit of a Piecewise-Defined Function at a Pointĭiscuss the existence of l i m  →  𝑓 ( 𝑥 ) given